• HOME
• FORUM
• SEARCH
• CONTACT

• HOME
• 4. Assembly Language Programming
• Data Transfer and Addressing Modes
  • Data Transfer Introduction
  • Register-Indirect Addressing
  • PC-Relative Addressing
  • Pre-indexed Addressing
  • Post-indexed Addressing
  • Byte Load and Store
• Shift and Rotate Instructions
  • Shift and Rotate Introduction
  • Logical Shift Operations
  • Arithmetic Shift Operations
  • Rotate Operations
• Putting It All Together
  • Flowcharts for Assembly Language Programming
  • Example Program

Arithmetic Shift Operations

ARM has two arithmetic shift operations, namely ASL (Arithmetic Shift Left) and ASR (Arithmetic Shift Right).

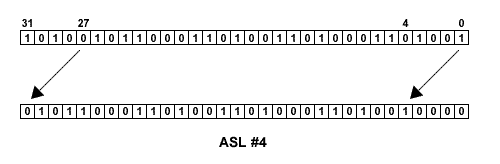
ASL is an arithmetic shift left by 0 to 31 places. The vacated bits at the least significant end of the word are filled with zeros. It is identical to LSL. In code terms, it is written in the same syntactic form:

MOV	r0, r1, ASL #3	; shift value in r1 3 places left and fill in vacant slots with 0's
MOV	r0, r1, ASL r2	; shift value in r1 by number of places given in r2 and fill in vacant slots with 0's

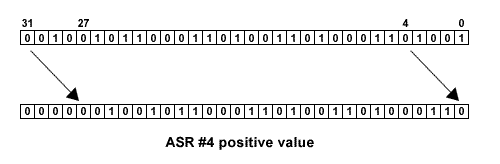
ASR is an arithmetic shift right by 0 to 32 places. The vacated bits at the most significant end of the word are filled with zeros if the original value (the source operand) was positive. The vacated bits are filled with ones if the original value was negative. This is known as "sign extending" because the most significant bit of the original value is the sign bit for 2's complement numbers, i.e. 0 for positive and 1 for negative numbers. Arithmetic shifting therefore preserves the sign of numbers.

MOV	r0, r1, ASR #3	; shift value in r1 3 places right and fill in vacant bits with copies of original most significant bit
MOV	r0, r1, ASR r2	; shift value in r1 right by number of places given in r2 fill in vacant bits with copies of original most significant bit

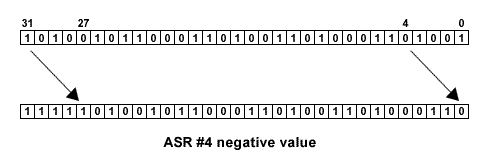
To show the difference between logical and arithmetic right shifts, consider a LSR and an ASR where the value to be shifted is 112 and the shift is 3 places. To keep the mathematics simple, we will use 8-bit numbers.

The bit pattern for 112 is 0111 0000. Performing LSL #3 transforms the bit pattern to be 0000 1110 (or 1410 which is 112 / 2^3). Performing ASL #3 again transforms the bit pattern to 0000 1110 (or 1410).

Now what happens if the number is -112?

First create the 2's complement bit pattern for -112 by flipping the bit pattern of 112 and adding 1:

0111 0000 becomes 1000 1111 + 1 becomes 1001 0000

Now perform a LSR #3 operation on 1001 0000. This shifts the bits 3 places to the right and fills in the vacated bits with 0s:

1001 0000 becomes 0001 0010 which is +1810

Now instead perform an ASR #3 operation on 1001 0000. This shifts the bits 3 places to the right and fills the vacated bits with copies of the most significant bit, i.e. 1's.

1001 0000 becomes 1111 0010 which is -1410. Thus this ASR operation is equivalent to performing -112 / 2^3.